
Gioca Puzzle Online
Nel tutorial seguente vengono presentate tecniche di base e avanzate per risolvere i puzzle Futoshiki passo dopo passo, con illustrazioni accompagnate per mostrare i metodi su specifiche configurazioni della scheda.
Il punto di partenza per raggiungere una soluzione è la definizione del gioco stesso: Futoshiki richiede all'utente di scoprire una tavola dove ogni cifra appare una volta su ogni riga e colonna, rispettando le disuguaglianze delle tavole. Utilizzando questo criterio, si possono compiere progressi verso una soluzione completando, passo dopo passo, quadrati vuoti con cifre specifiche perché sono l'unico modo per rispettare le restrizioni delle schede.
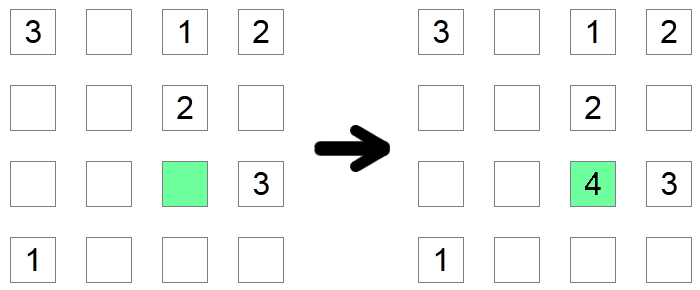
Se una colonna e una riga di quadrati contengono già tutte le cifre possibili, tranne una, allora quel quadrato deve contenere la cifra mancante. Nell'esempio precedente, il quadrato verde deve essere 4 poiché non sarebbe consentito avere alcun altro valore poiché le altre cifre possibili si trovano già nella sua riga o nella sua colonna.
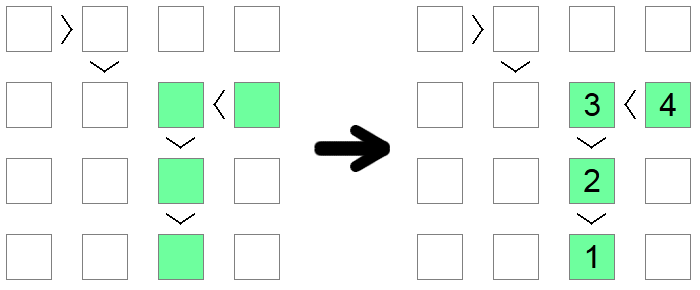
Se si nota una catena di disuguaglianze, sia < (tutte ascendenti) o > (tutte discendenti), uguali in dimensioni con le dimensioni delle tavole, allora quella catena deve essere una sequenza da 1 fino alla lunghezza della tavola. La lunghezza della catena garantisce che questa sequenza sia l'unica soluzione possibile che soddisfi la condizione monotona imposta dalla catena disuguaglianza.
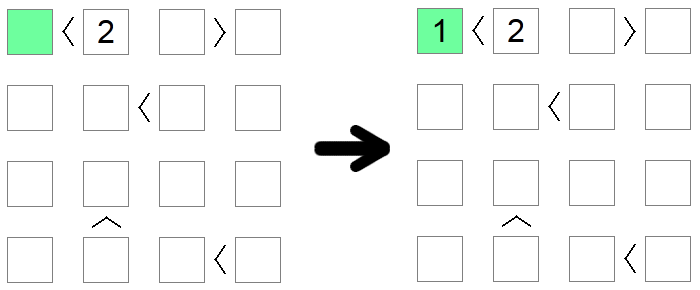
I quadrati inferiori a 2 devono avere implicitamente il valore 1 in quanto è l'unico valore ammissibile sulla tavola che rispetta tale condizione. Allo stesso modo, i quadrati che sono maggiori della dimensione della scheda meno 1 devono essere uguali alla dimensione della scheda. Nell'esempio precedente, l'unico valore possibile per il quadrato verde (meno di 2) è 1.
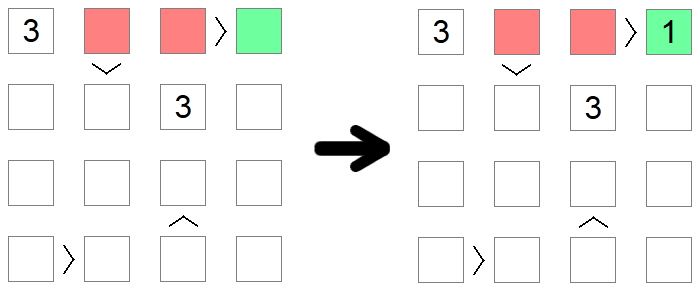
I quadrati che sono maggiori di altri quadrati non possono essere 1, il valore più basso consentito sulla scheda, in quanto non esiste un valore inferiore a 1. Allo stesso modo, i quadrati inferiori agli altri quadrati non possono contenere il valore massimo consentito, poiché non ci sarebbe nulla di più grande da riempire sull'altro lato della disuguaglianza. Nell'esempio precedente, 1 non può essere riempito nei quadrati rossi in quanto sono tutti maggiori degli altri quadrati di bordo, quindi l'unico posizionamento possibile per 1 sulla prima riga della tavola è il quadrato verde.
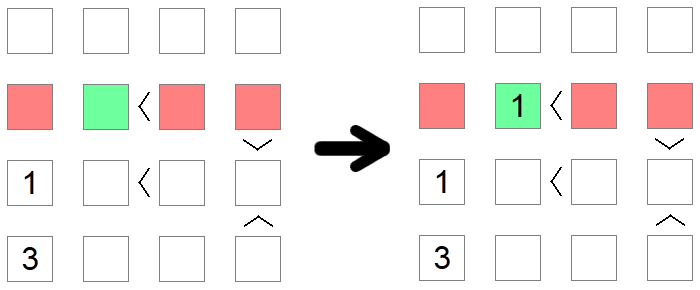
A volte è necessario utilizzare più regole per giungere a una conclusione. Questo è il caso nell'esempio sopra, dove proviamo a posizionare il valore 1 sulla seconda riga della scheda. Il primo quadrato rosso viene eliminato a causa di un' esclusione di colonne (abbiamo già un 1 su quella colonna), mentre il secondo e il terzo quadrato rosso vengono eliminati a causa dell'esclusione dei valori minimi in quanto tali luoghi hanno maggiori delle disuguaglianze ad essi associate. Pertanto il quadrato verde rimane l'unico posto possibile per posizionare 1 in quella fila.
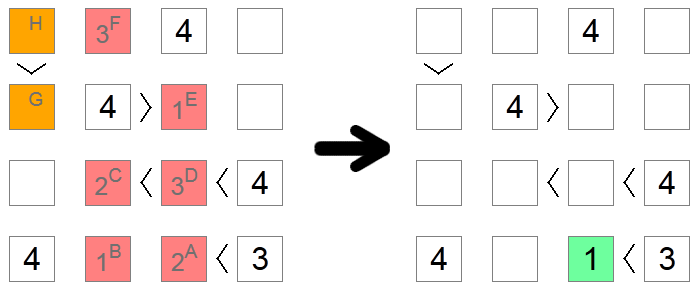
A volte, specialmente su tavole difficili, non ci sono altri modi per capire la cifra corretta per un quadrato tranne che per immergersi nelle implicazioni di ogni possibilità fino a raggiungere una contraddizione. Nell'esempio precedente, tutti i quadrati rossi e arancioni sono inizialmente vuoti. Vogliamo capire se il quadrato A contiene 1 o 2 . Supponiamo che contenga 2 e controlliamo per vedere se raggiungiamo una contraddizione basata su questa ipotesi.
Se il quadrato A ha un 2, allora il quadrato B avrebbe un 1(l'unico valore rimanente sulla riga inferiore). Il quadrato C può essere 1 o 2 in quanto ha una catena di disuguaglianze che richiede di avere a disposizione 2 numeri maggiori, ma ora non può essere 1 a causa dell'esclusione della colonna del quadrato B, quindi il quadrato C è un 2, e il quadrato D è un 3 (l'unico valore compreso tra 2 e 4). A causa delle esclusioni delle colonne, il quadrato E è 1 e il quadrato F è 3 .
Ora, se guardiamo i quadrati arancioni, notiamo la contraddizione: se il quadrato G dovesse essere 2, il quadrato H dovrebbe essere 3 o 4, che non sono consentiti a causa di un'esclusione di riga. Se il quadrato G dovesse essere 3, il quadrato H dovrebbe essere 4 che non è consentito a causa della stessa ragione. Poiché non abbiamo più valori rimanenti per il quadrato G, significa che abbiamo raggiunto un punto morto e la nostra ipotesi iniziale era sbagliata: 2 non è una mossa valida per il quadrato A, quindi possiamo andare avanti e metterci 1 in esso, l'unico altro valore possibile.
Weve mostrato sopra come risolvere un puzzle Futoshiki con successo coprendo una gamma di tecniche che possono aiutare a dedurre la mossa successiva anche in situazioni difficili. L'altro ingrediente chiave per diventare abile e veloce nel risolvere i puzzle Futoshiki è l'esperienza: più si pratica, migliore e più veloce si diventa.
Se sei per una sfida, si può giocare in questo momento un puzzle Futoshiki casuale cliccando sul pulsante qui sotto. Buona fortuna!
© 2024 - Tutti i diritti riservati - A proposito di - Informativa sulla privacy - DE | EN | ES | FR | IT | LV | NL | PL | PT | RO | SV | TR